After five weeks of nearly non-stop computation, a new record for the computation of the value \Gamma\left(\tfrac14\right) has been set: 500 billion digits of precision computed with Alexander Yee’s y-cruncher. This is the Gamma function, which when evaluated with the input \tfrac14, results in 3.62560990822\ldots1See: https://en.wikipedia.org/wiki/Particular_values_of_the_gamma_function#General_rational_argument
Motivation
There isn’t a practical need for such an absurd number of digits, but I wanted to stress test my new server while also gaining bragging rights for having beaten Dr. Ian Cutress‘s previous record of 362,560,990,822 decimal digits computed in 6 days on his very expensive EPYC server.
Unfortunately, that’s about it for the motivation section.
Hardware
This computation was completed with the spare computing power of the very server that is serving you this webpage. Below is an annotated picture of the hardware involved:

The computer used in this computation is a Dell PowerEdge R730xd with dual Intel Xeon E5-2690 v4 CPUs and 320 GB of RAM. An astute reader may notice that the amount of memory is insufficient to compute such a large number of digits – in fact, the memory requirement is nearly three terabytes. This is why y-cruncher has a built-in swapping functionality that is optimized for such computation.2Operating system swapping has no knowledge of y-cruncher’s memory access patterns, resulting in thrashing that greatly slows down the computation.
For swap, I obtained eight used 900 GB 10k RPM SAS hard drives. The combined throughput of all eight drives was approximately 1.5 GB/s in an application-level RAID0.3Why not use SSDs? These computations require a massive amount of data transfer – enough to significantly shorten the lifespan of most SSDs on the market. See y-cruncher’s FAQ. While only 3 TB of the 7.2 TB of drives was needed for the computation, y-cruncher greatly benefits from increased swap throughput.
Actually, I lied. The first half of the first computation4To make it onto the records page, y-cruncher requires two computations using independent formulas. This ensures the digit output is correct and wasn’t affected by hardware or software bugs. was done with two spare hard drives, the internal ZFS pool, and an internal NVMe SSD (obtained for an unrelated project) all in an application-level RAID0. Here’s an annotated picture of the previous setup:

This swap arrangement provided approximately 500 MB/s of combined throughput, which is far from optimal. Additionally, the USB-SATA bridge (“toaster”) wasn’t very stable, and interrupted the computation every two days or so as it dropped out of the system. When the new hard drives arrived, I used md-raid to create four RAID0 arrays of two hard drives each and symlinks to allow the existing computation’s checkpoint to utilize the much higher throughput of the 10k RPM SAS drives.
Initial computation
The initial computation was performed with the Series-Pi (Brown 2009) algorithm, implemented by Alexander Yee in y-cruncher as a custom formula. This computation took 20 days.
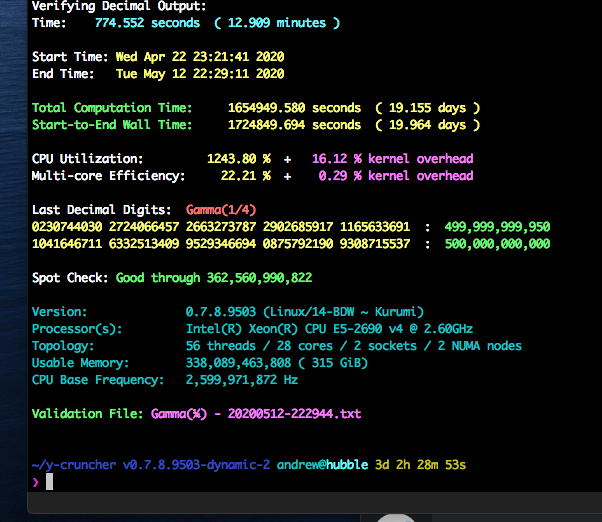
Verification
The verification computation was performed with the Lemniscate formula, also implemented by Alexander Yee as a custom formula. This computation took 15 days.
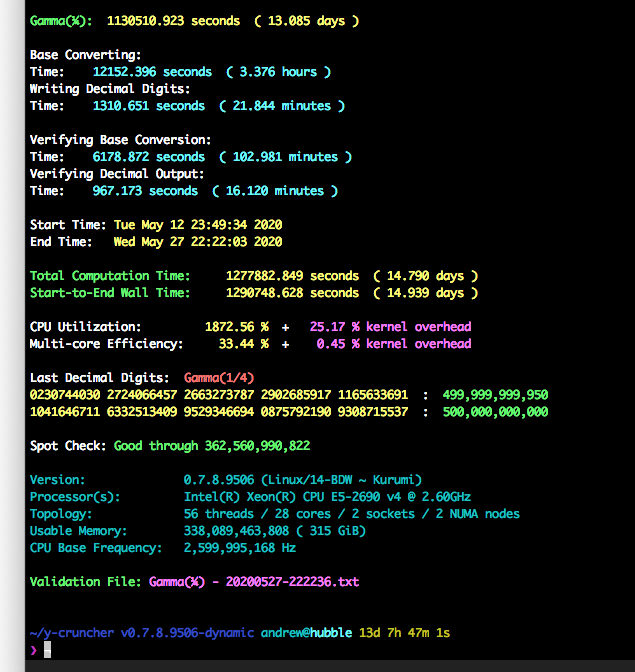
Environmental considerations
The computation used a large amount of energy and required a large amount of hardware. This is partially offset by the electricity supplier sourcing its energy from 100% renewable energy, and most of the hardware involved (including the R730xd and hard drives) is reused hardware that was previously decommissioned.
Timeline
- 2020-04-09: R730xd arrives and replaces the previous R710
- 2020-04-22: Computation begins with Series-Pi algorithm
- 2020-04-24: Computation is interrupted by the toaster crashing
- 2020-04-27: The toaster crashes again
- 2020-05-05: Necessary hardware arrives to allow for the new hard drives to be used for the computation
- 2020-05-09: The toaster crashes again, breaking the symlinks allowing y-cruncher to access the new drives
- 2020-05-09: Computation of Pi with Ramanujan algorithm begins
- 2020-05-12: Computation of Pi finishes, end of Series-Pi computation
- 2020-05-12: Verification begins with Lemniscate formula algorithm
- 2020-05-25: Lemniscate constant computation finishes, begin Pi computation with Chudnovsky algorithm
- 2020-05-27: End of Pi computation and the Gamma(1/4) calculation. The digits match, and the record appears to be broken!
If, for some reason, you need to access the decimal digit output (196 GB compressed), please contact me.
- 1
- 2Operating system swapping has no knowledge of y-cruncher’s memory access patterns, resulting in thrashing that greatly slows down the computation.
- 3Why not use SSDs? These computations require a massive amount of data transfer – enough to significantly shorten the lifespan of most SSDs on the market. See y-cruncher’s FAQ.
- 4To make it onto the records page, y-cruncher requires two computations using independent formulas. This ensures the digit output is correct and wasn’t affected by hardware or software bugs.

